Forschung am Lehrstuhl für Angewandte Mathematik III

Der Lehrstuhl für Angewandte Mathematik III gehört zum Bereich Modellierung, Simulation und Optimierung des Departments Mathematik. Die Arbeitsgruppe positioniert sich im Bereich Wissenschaftliches Rechnen. Thematische Schwerpunkte liegen in der Strömungsmechanik und der Bildverarbeitung.

Strömungsmechanik

Auch wenn wir uns dessen nicht immer bewusst sind, Strömungen umgeben uns und haben Einfluss auf unser Leben. Man denke nur an das Wetter bzw. Klima oder (auf kleinerem Maßstab) an Strömungen im menschlichen Körper wie den Blutfluss durch Adern oder die Luftströmung durch unsere Lungen. Übrigens ist die Simulation in diesen beiden Bereichen von großer Bedeutung, bei ersterem jedem geläufig durch den täglichen Wetterbericht.

Strömungen begegnen uns natürlich auch in mehr technischen Feldern. Beispiele sind hier: Fahrzeugumströmungen, Akustik, Hydraulik und vieles mehr.

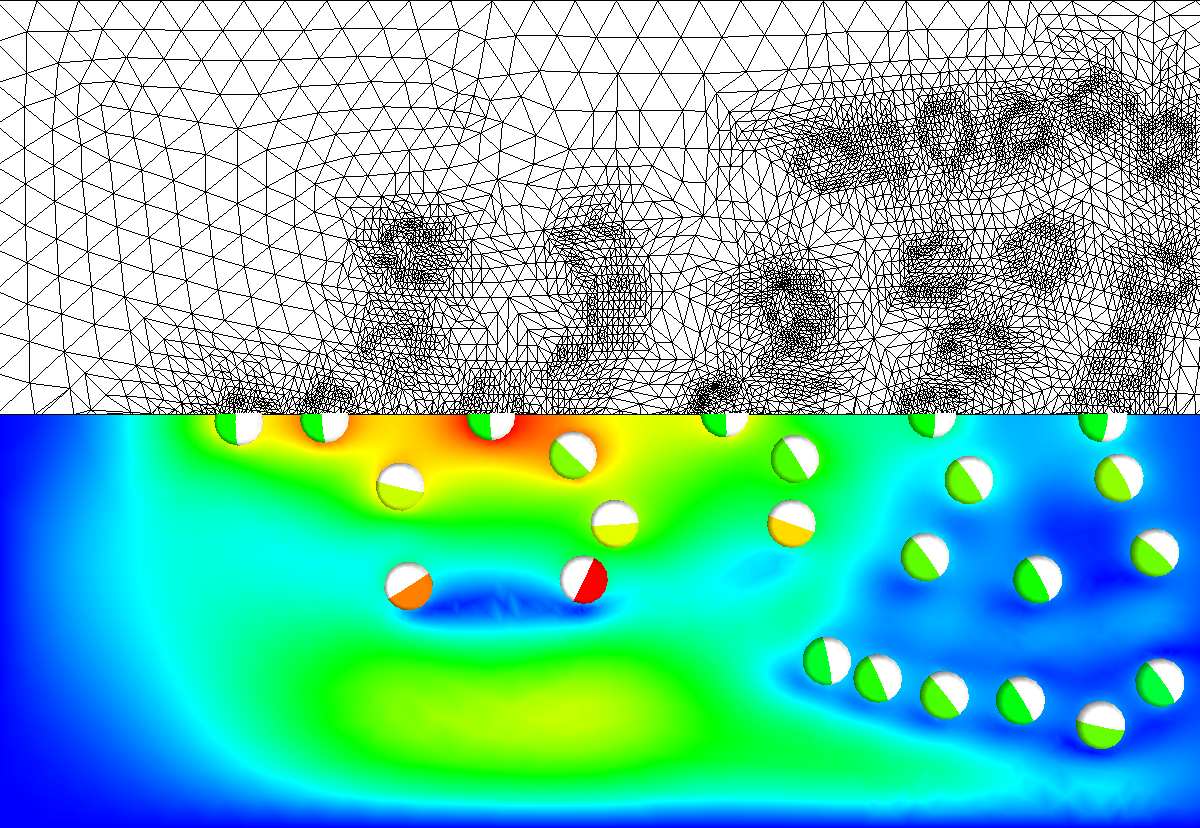
Die Bedeutung der Simulation liegt nun darin, dass sie teure Experimente ersetzen kann (wenigstens teilweise), eine Vielzahl von physikalischen Größen liefert, die experimentell nur schwer zugänglich sind und auch dort Studium von Szenarien zulässt, wo dies experimentell nur schwer oder überhaupt nicht möglich ist. Man denke dabei nur an die o.g. Klimaberechnung und Untersuchungen im medizinischen Bereich.

Allen Strömungen ist gemeinsam, dass sie sich im Wesentlichen mathematisch durch dieselben Gleichungen beschreiben lassen. Dies sind die sogenannten Navier-Stokes Gleichungen, ein ebenso interessantes wie schwieriges System von partiellen Differentialgleichungen. Unterscheidungen ergeben sich dadurch, ob die betrachteten Strömungen kompressibel sind und wie wichtig viskose, d.h. reibungsbehaftete, Effekte sind.

Abschließend sei bemerkt, dass die Strömungssimulation ein hochspannendes Feld interdisziplinärer Forschung darstellt, in dem Mathematiker fruchtbar mit Ingenieuren, Physikern und Informatikern zusammenarbeiten.