Eine DG Methode für das Subjective Surface Problem
Eine DG Methode für das Subjective Surface Problem
Teilnehmer
AM 3
- Michael Fried
AM 1
- Vadym Aizinger
AM
- Leon Bungert
Beschreibung
Ein grundlegendes Problem der Bildanalyse ist die Segmentierung, das heißt die Identifikation unterschiedlicher Regionen in einem gegebenen Bild. Abhängig vom Anwendungsfall können diese Regionen sich beispielsweise durch verschiedene Farben oder Graustufen, durch Texturen und durch Menge und Art eventuell vorhandenen Rauschens oder andere Dinge unterscheiden. Ihre Ränder können auch mehr oder weniger deutlich erkennbare Kanten im Bild darstellen. Häufig hängen die gesuchten Regionen direkt mit den im Bild dargestellten Objekten zusammen. Kanten von Objekten im Bild können durch Überdeckung, durch Rauschen oder fehlende Bildinformation unterbrochen oder zerstört sein.
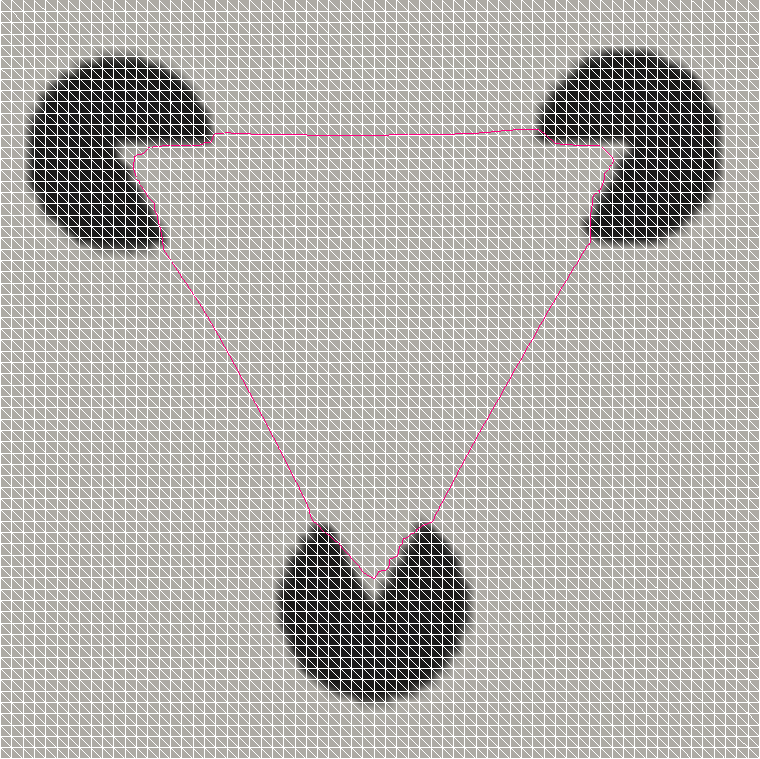
Auf ähnlich Weise können Objekte durch subjektive, also objektiv nicht vorhandenen, Konturen dem menschlichen Betrachter sichtbar werden, wie etwa beim aus der Psychologie bekannten Kanizsadreieck. Diese Situation wird Subjective Surface Problem genannt.
In diesem Projekt wird eine lokale DG Methode für das Subjective Surface Problem in einer Level-Set Darstellung formuliert und evaluiert. Eine neue gemischte Formulierung der Level-Set Gleichungen wird vorgeschlagen, welche die Behandlung der Nichtlinearität vereinfacht. Der dazu vorgeschlagene numerische Algorithmus wird durch Anwendung auf verschiedene künstliche und realistische Testsituationen evaluiert und mit einem älteren Finite Elemente Ansatz von Mikula und Fried verglichen.
Ergebnisse
Die Anwendbarkeit wird sowohl durch Vergleiche bei bekannten analytischen Lösungen als auch durch numerische Benchmarks und für einfache medizinische Datensätze sichergestellt. Dabei zeigt sich, das die LDG Methode zur Lösung des Subjective Surface Problems sehr gut geeignet ist und Ergebnisse liefert, die mit den entprechenden Ergebnissen des Finite Elemente Algorithmus‘ vergleichbar sind. Gleichzeitig vermeidet die LDG Methode dabei die im FE Algorithmus auftretenden falschen Peaks in der numerischen Lösung. Stückweise lineare DG Aproximationen sind auf gröberen Gittern den stückweise konstanten DG Approximationen vorzuziehen. Die erzielten Ergebnisse ermutigen eine Übertragung der Methoden auch auf komplexere oder 3D Situationen.