Nicht-Newtonsche Zweiphasenströmung in einem industriellen Befüllungsprozess

Teilnehmer

AM 3

• Eberhard Bänsch
• Ina Schüssler

Beschreibung

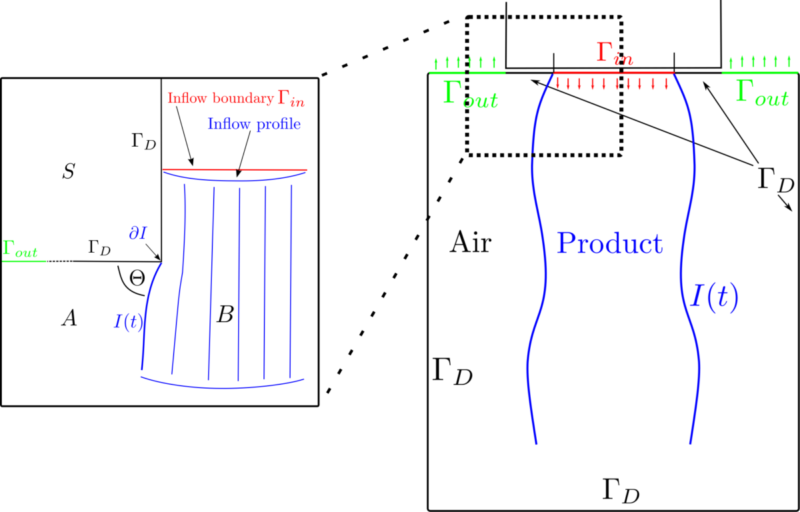
In diesem Projekt wurden ein Finite-Elemente-Modell einer Zweiphasenstömung entwickelt und implementiert. Das Modell besteht aus zwei Phasen – die eine ist ein nicht-newtonsches Fluid, die andere Luft – und der mathematischen Beschreibung der Oberfläche zwischen den Phasen (Interface). Der Fluss wird mit Hilfe der Navier-Stokes-Gleichungen erfasst, die allerdings abgewandelt sind, um die nicht-newtonschen Eigenschaften des Fluids zu beschreiben. Diese Eigenschaften werden durch das Carreau-Gesetz beschrieben, einem Potenzgesetz, das es erlaubt, die strukturviskosen Eigenschaften des Fluids zu modellieren.

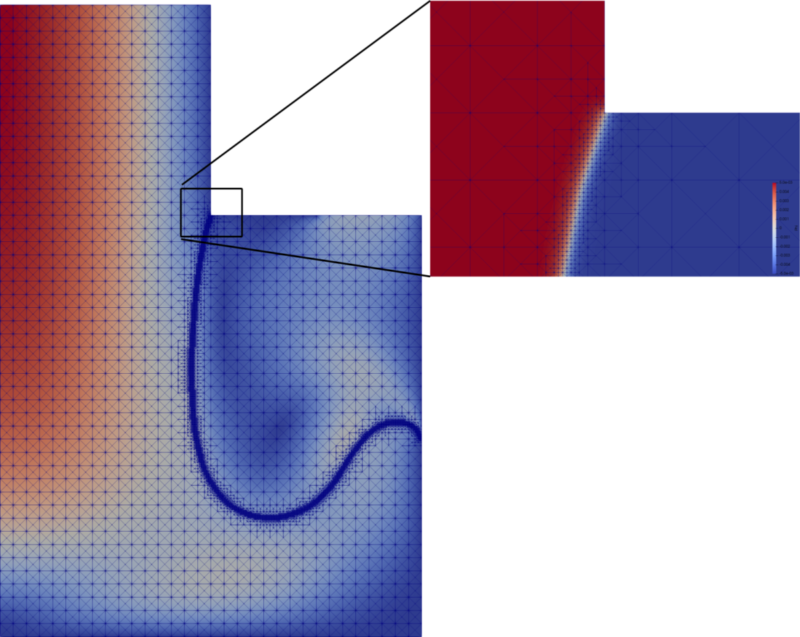
Die Levelset-Methode wurde entwickelt, um die Bewegung des Interfaces darzustellen. Dabei wurde eine implizite Reinitialisierungstechnik benutzt, bei der die rechte Seite der Levelset-Gleichung verändert wird (dabei folge ich dem Paper \ref{Bonito}). Die Genauigkeit mit der das Interface repräsentiert werden kann, hängt von einer delta-Funktion ab, die unter anderem von der Levelsetfunktion und der Auflösung des Gitters um das Interface herum abhängt. Die Breite der delta-Funktion beeinflusst unter anderem die Genauigkeit der numerischen Berechnung der Oberflächenspannung.

Der Einfüllprozess findet in einem bewegten Gebiet statt. Das führt dazu, dass auch das zugrundeliegende Gitter bewegt wird und – bei zu großer Bewegung – neu erstellt werden muss. Die Gitterbewegung wird in den Gleichungen durch eine ALE-Transformation erfasst.

Referenzen

• A. Bonito, J.-L. Guermond, S. Lee (2016). Numerical Simulations of Bouncing Jets. Numerical Methods in Fluids, 80: 53-75.