Interaktives Hochleistungsrechnen
Interaktives Hochleistungsrechnen (HPC)
Teilnehmer
AM 3
LS 10 (Informatik)
- Marco Heisig
Beschreibung
Probleme im Bereich des Hochleistungsrechnens sind großskalige industrielle Problem, Probleme in hochdimensionalen Räumen oder mit hohen Genauigkeitsanforderungen, große Parameterstudien und Optimierungsprobleme oder eine Kombination von all diesen Varianten. Oft kommen diese Probleme auch Forschungsbereichen am Rande des bekannten Wissens, so dass ein explorativer Zugang wesentlich für ihre effiziente Lösung ist.
Der übliche HPC-Ansatz zur Lösung dieser Probleme besteht in der Anwendung von sehr effektiver, aber problem- und hardware-spezifischer statisch kompilierten Anwendungsprogrammen in einer Batch-artigen Umgebung, und ist nicht gut für explorative Problemlösung geeignet. Daher schlagen wir einen neuen Zugang vor, der Interaktivität über die ganze Anwendung beinhaltet, wobei der Kern dabei ist die interaktive Computersprache Common Lisp zu verwenden, welche dynamisch und zur Laufzeit schnellen Maschinencode generieren kann.
In Common Lisp haben wir das freie Software-Framework Femlisp zur Lösung partieller Differentialgleichungen entwickelt. Eine parallele objekt-orientierte Bibliothek namens DDO/CL-MPI schirmt dabei den Femlisp-Benutzer/Programmierer von der parallelen Hardware an.
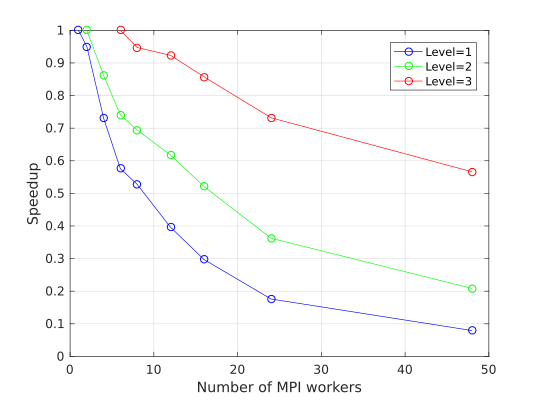
Wir haben diesen Ansatz für die Berechnung eines effektiven Koeffizienten eines 3D-Elastizitätsproblems verwendet. Das erste Bild unten zeigt ein Verschiebungsfeld für eine repräsentative Zelle, die einer bestimmten Krafteinwirkung unterworfen wurde. Das zweite Bild zeigt den parallelen Speedup für diese Rechnung auf einem Linux-Cluster.