Marangoni-Konvektion
Teilnehmer
AM 3
- Eberhard Bänsch
- Kathrin Bäumler
Extern
- A. Paschedag
- M. Wegener
Anwendung
In flüssig/flüssig Extraktionsprozessen ist das Ziel eine in einer Flüssigphase enthaltene Substanz in eine andere, normalerweise nicht mischbare, Flüssigphase zu überführen. Dazu wird die eine Phase in der anderen dispersiert und der Massenübergang geschieht dann entlang der Grenzschicht der dispersen Tropfen. Da dieser Prozess ein wichtiger Bestandteil vieler industrieller Anlagen ist, besteht ein großes Interessse die Extraktionsleistung zu simulieren und zu optimieren.
Vorhersagen von Haltezeiten, Massenübergangskoeffizienten, der Einfluß von Tensiden, etc. sind nicht immer befriedigend, insbesondere wenn Marangonikonvektion eine Rolle spielt. Da eine analytische Beschreibung oft nicht verfügbar ist und da Experimente kosteninstensiv sind, sind gute numerische Simulationen wichtig, die mit den Schwierigkeiten dieser komplexen Zweiphasen-Strömungsprobleme fertig werden.
Mathematisches Modell
Die Zweiphasenstrümung wird durch die Navier-Stokes-Gleichung für unmischbare, inkompressible, Newtonsche Strömungen in den Phassen Ωj modelliert. Der Massentransfer wird durch eine Konvektions-Diffusion-Gleichung modelliert.
- ρj ∂t uj + ρj ( uj ·∇) uj -Δ uj +∇ pj = ρj fj
- ∇· uj = 0
- ∂t cj +( uj ·∇) cj -Δ cj = 0
Die Unbekannten u,p,c sind Geschwindigkeit, Druck und Konzentration. Der Index j bezeichnet die Phase (d für die disperse und c für die kontinuierliche Phase). f beschreibt äußere Kräfte (hier Gravitation). Materialparameter sind Dichte ρ , dynamische Viskosität μ und der Diffusionskoeffizient D.
Die Interface-Bedingungen auf dem Interface Γ haben die Form:
- [u] = 0
- [σν] = γκν- ∇S γ(c)
- [D∇c·ν] = 0
- cc = H cd
Hier bezeichnet σ=μ(∇u+ (∇ u) Τ )-pI den Spannungstensor, ν die Normale von Γ (von Ωc nach Ωd zeigend), κ ist die Summe der Hauptkrümmungen, mit der Konvention, dass κ>0 wenn Ωd konvex ist. V_Γ bezeichnet die Geschwindigkeit von Γ in Richtung von ν und ∇ s ist der Oberflächengradient. Die Klammern [⋅] bezeichnen den Sprung einer Größe über Γ , und H heißt Partitionskoeffizient oder auch Henry-Koeffizient.
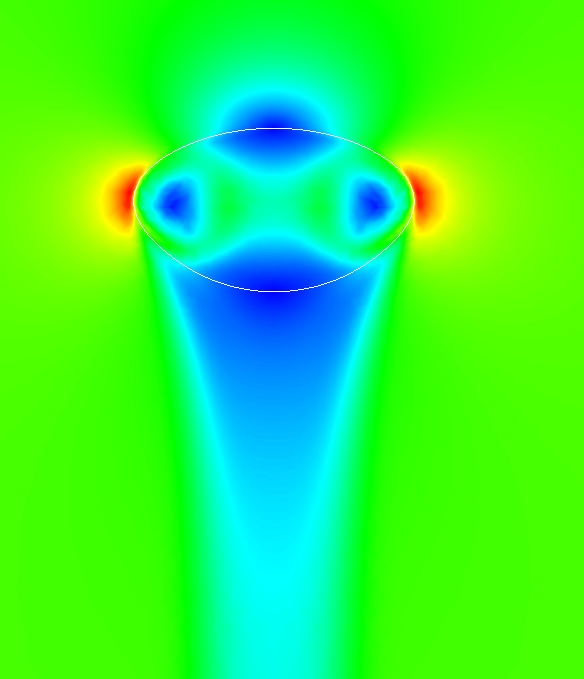
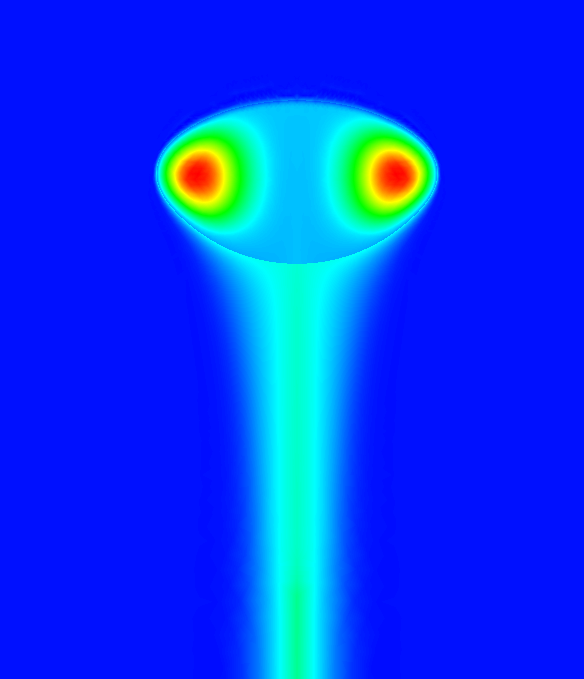
Die Gleichung mit dem Oberflächengradient koppelt das Geschwindigkeitsfeld mit der Konzentration der gelösten Substanz, was zu konzentrationsabhängigen konvektiven Mustern führt, die man Marangoni-Konvektion nennt.
Numerical method
Die Zweiphasenströmung wird mit dem Code NAVIER gelöst, der um folgende Merkmale erweitert wurde:
- Unterraumprojektion, eine effiziente Implementation der Interface-Bedingungen, geeignet für das simultane Lösen des Problems in beiden Phasen.
- SUPG – Streamline Upwind Petrov Galerkin wird für eine bessere Stabilität des konvektions-dominierten Massentransfers verwendet.
- Grad-Div-Stabilisierung für die Navier-Stokes equation.