Zeitliche Mehrskalenmethoden für ein Atherosklerose-Modell
Zeitliche Mehrskalenprobleme für ein Atherosklerose-Modell
Teilnehmer
AM 3
Beschreibung
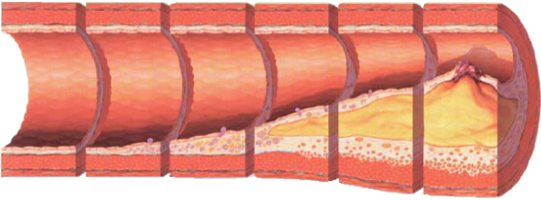
Stadien der Atherosklerose, Bild-Lizenz CC BY-SA 3.0, Original
Atherosklerose ist eine Krankheit bei der sich, durch eine Kette von biologischen und mechanischen Prozessen, Plaque in den Arterienwänden bildet und anwächst. Ein Aspekt des Plaque-Wachstums ist der Einfluss von Kräften durch den pulsierenden Blut-Fluss auf die Oberfläche der Wand. Direkte numerische Simulationen solcher Modelle ist auf realistischen Zeitskalen des Wachstums, Monate oder Jahre, nicht möglich, denn jeder einzelne Herzschlag müsste simuliert werden.
Das Ziel dieses Projekts ist die rigorose Herleitung von Plaque-Modellen, welche eine Simulation auf langen Zeitskalen zulassen. Dies geschieht durch die Interpretation des Originalproblems als singulär gestörtes System von partiellen Differentialgleichungen mit periodischer Blut-Einströmung. Durch rigorose Herleitung eines Grenzsystems und die Quantifizierung der Konvergenzrate in dem Perturbationsparameter erhalten wir ein Modell, welches das Originalproblem gut approximiert und eine numerische Langzeitsimulation erlaubt. Das Verhalten und die Eigenschaften dieses Grenzsystems werden numerisch studiert.