Arbeitsgruppe und Forschung

Research Interests

The general research interests of the group lie in applied analysis, more precisely in the calculus of variations, nonlinear PDEs, and the mathematical modeling of problems in materials science. Research questions and mathematical techniques include:

  • Multiscale Methods
  • Gamma-convergence, relaxation, and integral representation
  • Free-discontinuity problems
  • Atomistic models and discrete-to-continuum limits
  • Crystallization
  • Geometric rigidity and linearization
  • Functions of bounded variation/deformation
  • Geometric measure theory
  • Nonlinear evolution equations

Research group and associated members:

 

Former members:

Main research directions

The current main research directions of the group are

Variational problems involving bulk and surface energies

    • People: Marco Bresciani, Antonio Donnarumma, Manuel Friedrich, Joscha Seutter
    • Funding:  GRK IntComSin, DFG-grant „Fracture models in SBD“ (2019-2021)

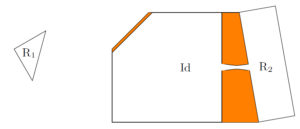
                                     Geometric (non-)rigidity in variable domains (Friedrich, Kreutz, Zemas)

 

Atomistic systems and molecular structures

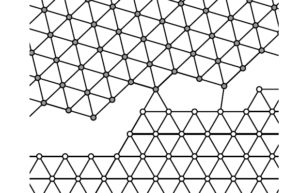
       Grain boundaries in polycrystals (Friedrich, Kreutz, Schmidt)

Evolutionary problems in solid mechanics

    • People: Rufat Badal, Manuel Friedrich, Lennart Machill
    • Funding: DFG grant „Effective theories for metric gradient flows in solid mechanics“ (2021 – 2024), DAAD grant „Rigorous derivation of linearized models in thermomechanics“ (2022-2023)
    • Latest paper: S. Almi, R. Badal, M. Friedrich, S. Schwarzacher: Thermo-elastodynamics of nonlinearly viscous solids.

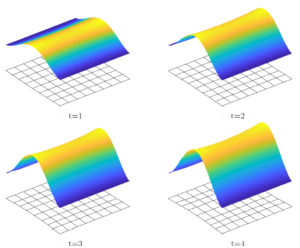
 Evolution of viscoelastic von Kármán plate (Friedrich, Kruzik, Valdman)

Publications

Publications of the group, ordered by topics:

Variational models of fracture and material failure

  • M. Bresciani, M. Friedrich: Quasistatic growth of cavities and cracks in the plane . Submitted 2024. [Preprint]
  • M. Bresciani, M. Friedrich, C. Mora-Corral: Variational models with Eulerian-Lagrangian formulation allowing for material failure. Submitted 2024. [Preprint]
  • M. Friedrich, C. Labourie, K. Stinson: Strong existence for free discontinuity problems in linear elasticity. Submitted 2024. [Preprint]
  • M. Friedrich, J. Seutter: Atomistic-to-continuum convergence for quasi-static crack growth in brittle materials. Submitted 2024. [Preprint]
  • M. Friedrich, C. Labourie, K. Stinson: On regularity for Griffith almost-minimizers in the plane. Submitted 2023. [Preprint]
  • C. Labourie, A. Lemenant: Epsilon-regularity for Griffith almost-minimizers in any dimension under a separating condition. Arch. Ration. Mech. Anal. 247 (2023), 105. [Preprint, Article]
  • R. Badal, M. Friedrich, J. Seutter: Existence of quasi-static crack evolution for atomistic systems. Forces in mechanics, to appear. [Preprint, Article]
  • S. Almi, E. Davoli, M. Friedrich: Non-interpenetration conditions in the passage from nonlinear to linearized Griffith fracture. J. Math. Pures Appl.175 (2023) pp. 1-36. [Preprint, Article]
  • M. Friedrich, M. Perugini, F. Solombrino: Gamma-convergence for free-discontinuity problems in linear elasticity: Homogenization and relaxation. Indiana University Mathematics Journal, to appear. [Preprint]
  • V. Crismale, M. Friedrich, F. Solombrino: Integral representation for energies in linear elasticity with surface discontinuities. Adv. Calc. Var. 15 (2022), pp. 705–733. [Preprint, Article]
  • M. Friedrich: Griffith energies as small strain limit of nonlinear models for nonsimple brittle materials. Mathematics in Engineering 2 (2020), pp. 75-100. [Preprint, Article]
  • M. Friedrich: A compactness result in GSBV^p and applications to Γ-convergence for free discontinuity problems. Calc. Var. PDE 58:86 (2019). [Preprint, Article]
  • M. Friedrich, F. Solombrino: Quasistatic crack growth in 2d-linearized elasticity. Ann. Inst. H. Poincaré Anal. Non Linéaire 35 (2018) pp. 27-64. [Preprint, Article]
  • M. Friedrich: A derivation of linearized Griffith energies from nonlinear models. Arch. Ration. Mech. Anal. 225 (2017) pp. 425-467. [Preprint, Article]

Epitaxially strained films and material voids

  • M. Friedrich, L. Kreutz, K. Zemas: Derivation of effective theories for thin 3D nonlinearly elastic rods with voids. Math. Models Methods Appl. Sci. (M3AS), to appear. [Preprint, Article]
  • (with L. Kreutz, K. Zemas) From atomistic systems to linearized continuum models for elastic materials with voids. Nonlinearity 36 (2023) pp. 679-735. [Preprint, Article]
  • M. Friedrich, L. Kreutz, K. Zemas: Geometric rigidity in variable domains and derivation of linearized models for elastic materials with free surfaces. Submitted 2021. [Preprint]
  • V. Crismale, M. Friedrich: Equilibrium configurations for epitaxially strained films and material voids in three-dimensional linear elasticity. Arch. Ration. Mech. Anal. 237 (2020), pp. 1041-1098. [Preprint, Article]
  • L. Kreutz, P. Piovano: Microscopic validation of a variational model of epitaxially strained crystalline film. SIAM J. Math. Anal. 53 (2021), pp. 453-490. [Preprint, Article]

Multiphase materials

  • A. F. Donnarumma: Gamma-convergence and stochastic homogenization of second order singular perturbation models for phase transitions. Submitted 2024. [Preprint]
  • M. Friedrich, A. F. Donnarumma: Stochastic homogenisation for functionals defined on asymptotically piecewise rigid functions. Submitted 2023. [Preprint]
  • M. Friedrich, L. Kreutz, B. Schmidt: Emergence of rigid polycrystals from atomistic systems with Heitmann-Radin sticky disk energy. Arch. Ration. Mech. Anal. 240 (2021), pp. 627-698. [Preprint, Article]
  • (with E. Davoli) Two-well linearization for solid-solid phase transitions. J. Eur. Math. Soc. (JEMS), to appear. [Preprint, Article]
  • M. Friedrich, M. Perugini, F. Solombrino: Lower semicontinuity for functionals defined on piecewise rigid functions and on GSBD. J. Funct. Anal. 280 (2021), 108929. [Preprint, Article]
  • M. Friedrich, F. Solombrino: Functionals defined on piecewise rigid functions: Integral representation and Γ-convergence. Arch. Ration. Mech. Anal. 236 (2020), pp. 1325-1387. [Preprint, Article]
  • E. Davoli, M. Friedrich: Two-well rigidity and multidimensional sharp-interface limits for solid-solid phase transitions. Calc. Var. PDE 59:44 (2020). [Preprint, Article]

Geometric rigidity, inequalities in the space SBD

  • S. Almi, M. Caponi, M. Friedrich, F. Solombrino: Geometric rigidity on Sobolev spaces with variable exponent and applications. Submitted 2023. [Preprint]
  • A. Guerra, X. Lamy, K. Zemas: Sharp quantitative stability of the Möbius group among sphere-valued maps in arbitrary dimension. Submitted 2023. [Preprint]
  • F. Cagnetti, A. Chambolle, M. Perugini, L. Scardia: An extension result for generalised special functions of bounded deformation. Journal of Convex Analysis 28 (2021), pp. 457-470. [Preprint, Article]
  • M. Friedrich: A piecewise Korn inequality in SBD and applications to embedding and density results. SIAM J. Math. Anal. 50 (2018), pp. 3842-3918. [Preprint, Article]
  • M. Friedrich: On a decomposition of regular domains into John domains with uniform constants. ESAIM Control Optim. Calc. Var. 24 (2018), pp. 1541-1583. [Preprint, Article]
  • M. Friedrich: A Korn-type inequality in SBD for functions with small jump sets. Math. Models Methods Appl. Sci. (M3AS) 27 (2017) pp. 2461-2484. [Preprint, Article]
  • M. Friedrich, B. Schmidt: A quantitative geometric rigidity result in SBD. Preprint 2015. [Preprint]

Crystallization and lattice energies

  • M. Friedrich, W. Górny, U. Stefanelli: The ℓ1 double-bubble problem in three dimensions. Submitted 2023. [Preprint]
  • M. Friedrich, W. Górny, U. Stefanelli: A characterization of ℓ1 double bubbles with general interface interaction. Submitted 2023. [Preprint]
  • M. Friedrich, L. Kreutz: A proof of finite crystallization via stratification. J. Stat. Phys. 190:199 (2023). [Preprint, Article]
  • M. Cicalese, L. Kreutz, G. P. Leonardi: Wulff-crystals in FCC and HCP lattices. Submitted 2021. [Preprint]
  • A. Chambolle, L. Kreutz: Crystallinity of the homogenized energy density of periodic lattice systems. Multiscale Modeling & Simulation 21 (2023), pp. 34-79.  [Preprint, Article]
  • M. Friedrich, W. Górny, U. Stefanelli: The double-bubble problem on the square lattice. Interfaces Free Bound. 26 (2024) pp. 79-134. [Preprint, Article]
  • (with L. Bétermin, U. Stefanelli) Lattice ground states for Embedded-Atom Models in 2D and 3D. Letters in Mathematical Physics 111: 107 (2021). [Preprint, Article]
  • M. Friedrich, U. Stefanelli: Crystallization in a one-dimensional periodic landscape. J. Stat.Phys. 179 (2020), pp. 485-501. [Preprint, Article]
  • M. Friedrich, L. Kreutz: Finite crystallization and Wulff shape emergence for ionic compounds in the square lattice. Nonlinearity 33 (2020), pp. 1240-1296. [Preprint, Article]
  • M. Friedrich, L. Kreutz: Crystallization in the hexagonal lattice for ionic dimers. Math. Models Methods Appl. Sci. (M3AS) 29 (2019), pp. 1853-1900. [Preprint, Article]

Geometry and stability of nanostructures

  • M. Friedrich, M. Seitz, U. Stefanelli: Tilings with nonflat squares: a characterization. Milan Journal of Mathematics 90 (2022), pp. 131-175. [Preprint, Article]
  • L. Bétermin, U. Stefanelli: Angle-rigidity for Z^2 configurations. Nonlinearity 34 (2021), pp. 8392-8413. [Preprint, Article]
  • M. Friedrich, U. Stefanelli: Ripples in graphene: A variational approach. Comm. Math. Phys. 379 (2020), pp. 915–954. [Preprint, Article]
  • M. Friedrich, E. Mainini, P. Piovano, U. Stefanelli: Characterization of optimal carbon nanotubes under stretching and validation of the Cauchy-Born rule. Arch. Ration. Mech. Anal. 231 (2019), pp. 465-517. [Preprint, Article]
  • U. Ludacka, M. R. A. Monazam, C. Rentenberger, M. Friedrich, U. Stefanelli, J. C. Meyer, J. Kotakoski: In situ control over graphene ripples and strain in the electron microscope. npj 2D Materials and Applications 2: 25 (2018). [Article]
  • M. Friedrich, U. Stefanelli: Graphene ground states. Zeitschrift für angewandte Mathematik und Physik, June 2018, 69:70. [Preprint, Article]
  • M. Friedrich, P. Piovano, U. Stefanelli: The geometry of C60: A rigorous approach via Molecular Mechanics. SIAM J. Appl. Math. 76 (2016) pp. 2009-2029. [Preprint, Article]

Spin systems

  • A. Bach, M. Cicalese, L. Kreutz, G. Orlando: The antiferromagnetic XY model on the triangular lattice: topological singularities. Indiana Univ. Mat. J. 71 (2022), pp. 2411-2475. [Preprint]
  • A. Bach, M. Cicalese, L. Kreutz, G. Orlando: The antiferromagnetic XY model on the triangular lattice: chirality transitions at the surface scaling. Calc. Var. PDE (2021), 60:149. [Preprint, Article]
  • A. Braides, L. Kreutz: Optimal design of lattice surface energies. Calc. Var. PDE 57, 97 (2018) [Preprint, Article]
  • A. Braides, L. Kreutz: Optimal bounds for periodic mixtures of nearest-neighbour ferromagnetic interactions. Rendiconti Lincei-Matematica e Applicazioni 28(1) (2017) 103–117 [Preprint, Article]

Cleavage laws in brittle crystals

  • M. Friedrich, B. Schmidt: On a discrete-to-continuum convergence result for a two dimensional brittle material in the small displacement regime. Netw. Heterog. Media 10 (2015) pp. 321-342. [Preprint, Article]
  • M. Friedrich, B. Schmidt: An analysis of crystal cleavage in the passage from atomistic models to continuum theory. Arch. Ration. Mech. Anal. 217 (2015) pp. 263-308. [Preprint, Article]
  • M. Friedrich, B. Schmidt: An atomistic-to-continuum analysis of crystal cleavage in a two-dimensional model problem. J. Nonlin. Sci. 24 (2014) pp. 145-183. [Preprint, Article]

Nonlinear viscoelasticity and thermoviscoelasticity

  • L. Machill: Thermo-elastodynamics of nonlinearly viscous solids. Submitted 2024. [Preprint]
  • S. Almi, R. Badal, M. Friedrich, S. Schwarzacher: Nonlinear relations of viscous stress and strain rate in nonlinear Viscoelasticity . Submitted 2024. [Preprint]
  • R. Badal, M. Friedrich, M. Kruzik, L. Machill: Positive temperature in nonlinear thermoviscoelasticity and the derivation of linearized models . Submitted 2024. [Preprint]
  • R. Badal, M. Friedrich, L. Machill: Derivation of a von Kármán plate theory for thermoviscoelastic solids. Submitted 2023. [Preprint]
  • M. Friedrich, M. Seitz, U. Stefanelli: Discrete-to-continuum linearization in atomistic dynamics. Submitted 2023. [Preprint]
  • M. Friedrich, L. Machill: One-dimensional viscoelastic von Kármán theories derived from nonlinear thin-walled beams.
    Calc. Var. PDE 62:190 (2023). [Preprint, Article]
  • R. Badal, M. Friedrich, M. Kruzik: Nonlinear and Linearized Models in Thermoviscoelasticity. Arch. Ration. Mech. Anal. 247: 5 (2023). [Preprint, Article]
  • M. Friedrich, L. Machill: Derivation of a one-dimensional von Kármán theory for viscoelastic ribbons. NoDEA Nonlinear Differential Equations Appl. 59:11 (2022). [Preprint, Article]
  • M. Friedrich, M. Kruzik: Derivation of von Kármán plate theory in the framework of three-dimensional viscoelasticity. Arch. Ration. Mech. Anal. 238 (2020), pp. 489-540. [Preprint, Article]
  • (with M. Kruzik, J. Valdman) Numerical approximation of von Kármán viscoelastic plates. DCDS-S, 14 (2021), pp. 299-319. [Preprint, Article]
  • M. Friedrich, M. Kruzik: On the passage from nonlinear to linearized viscoelasticity. SIAM J. Math. Anal. 50 (2018), pp. 4426-4456. [Preprint, Article]

Nonlocal problems

  • S. Almi, M. Caponi, M. Friedrich, F. Solombrino A fractional approach to strain-gradient plasticity: beyond core-radius of discrete dislocations. Submitted 2024. [Preprint]
  • M. Friedrich, M. Seitz, U. Stefanelli: Nonlocal-to-local limit in linearized viscoelasticity. Comm. Appl. Ind. Math., to appear. [Preprint]