weitere Optimierungsprojekte
weitere Optimierungsprojekte
|
EFI Synthetic Biology (2014-2016) Das Projekt kombiniert die Disziplinen der Biologie, Chemie, Informatik, Mathematik, Physik und der Ingenieurwissenschaften in interdisziplinären Forschungsteams zur Entwicklung neuer Stoffwechselwege in lebenden Zellen und künstlichen Systemen. |
|
Details Klassische Beispiele der Synthetischen Biologie sind die Entwicklung maßgeschneiderter Minimalzellen, das Design neuartiger Stoffwechselwege, die Konstruktion komplexer genetischer Schalter und die Schaffung orthogonaler Biosysteme. Anwendung sollen diese Entwicklungen in der Krankheitsprävention, Diagnostik und Therapie, aber auch bei der Entwicklung neuer Quellen für Bioenergie, für den Umweltschutz und die Herstellung von Feinchemikalien finden. Das Projekt verfolgt die Ziele, die an der FAU vorhandene Expertise in den obengenannten Disziplinen zu bündeln und Projekte zum Design neuer Stoffwechselwege in lebenden Systemen sowie die Entwicklung maßgeschneiderter Minimalzellen und Nanofabriken zu fördern. |
| Weitere Informationen über EFI Synthetic Biology |
|
Optimization of iron oxide Pigments (2012-2017) The dependency of the optical properties of a pigment film and the shape or shape distribution of the pigment is studied within this project. Further, this dependency is used to identify regions in parameterized shape space which will lead to better color values of the pigment. |
|
Details The interaction of electromagnetic waves and material is mathematically described by Maxwell’s equations. Under the assumption of a time-harmonic incident light – which holds in the studied regime – this equations can be transformed to the well known curl-curl formulation of Maxwell’s equation. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr.-Ing. Wolfgang Peukert (Erlangen), Prof. Dr. Ulf Peschel (Erlangen), Prof. Dr. Robin N. Klupp Taylor (Erlangen), Dr. Lukas Pflug (Erlangen) |
|
Optimierungsverfahren in CAE-Tools (2012-2015) Dieses Projekt beschäftigt sich mit der speziellen Problemstellung, geeignete Optimierungsverfahren für den Bereich des Maschinenbaus zu entwickeln und diese so als integriertes Werkzeug in CAE-Anwendungen zur Verfügung zu stellen, dass die Anwender den überwiegenden Teil ihrer Optimierungsprobleme selbst formulieren und lösen können. |
|
Details In Industrieunternehmen ist eine Produktentwicklung ohne Unterstützung durch Software nicht mehr denkbar. Neben der effizienten Erstellung und Berechnung von komplexen Modellen ist die vollautomatisierte Optimierung von Parametern eines Produktes verstärkt in den Vordergrund gerückt. Hierbei handelt es sich z.B. um die Maximierung von Lebensdauern oder die Minimierung von Reibung. Auf dem kommerziellen Markt sind diverse universelle Optimierungswerkzeuge zu finden. Allerdings sind diese Produkte aufgrund Ihrer gewünschten vielseitigen Einsetzbarkeit für beliebige Optimierungsaufgaben in ihrer Bedienung sehr komplex und nur nach aufwändiger Einarbeitungszeit effizient nutzbar. Auch können hierbei spezielle Anforderungen von konkreten Aufgaben nur ungenügend berücksichtigt werden. Im Rahmen diese Projektes entsteht ein spezielles Optimierungswerkzeug „OptiKit“, das sich nahtlos in CAE-Programme des Kunden auf Basis eines Frameworks einfügen lässt. Auf diesem Wege steht es dem Anwender direkt als Teil des Entwicklungswerkzeugs zur Verfügung. Hierdurch wird eine umfassende Modellierung des Optimierungsproblems innerhalb der gewohnten grafischen Oberfläche ermöglicht. Als Teil dieser Modellierung können die Parameter und die Zielfunktion der Optimierung direkt aus dem CAE-Modell entnommen werden. Randbedingungen können, neben den Modell-inhärenten Bedingungen, vom Anwender frei hinzugefügt werden. Das Optimierungswerkzeug ist dabei so flexibel, dass es mit rein gleitkommazahligen Problemen ebenso umzugehen vermag wie mit rein ganzzahligen oder auch gemischt-ganzzahligen Problemen. Damit ist es in der Lage, die Optimierungsprobleme zu behandeln, die im Umfeld der Produktauslegung im Maschinenbau auftreten. Eine integrierte Robustheitsbewertung während der Optimierungsrechnung ist zuschaltbar, um z.B. Fertigungstoleranzen oder schwankende Umwelteinflüsse abzusichern. Zur Flexibilisierung stehen dem Endanwender mehrere verschiedene Optimierungsverfahren mit unterschiedlichen Stärken und Schwerpunkten zur Verfügung. So können je nach Problemtyp neben evolutionären Algorithmen auch numerische Richtungssuchverfahren oder an DoE angelehnte Verfahren zum Einsatz kommen. Darüber hinaus werden spezielle Optimierungsverfahren entwickelt und implementiert, die auf die Anforderungen der relevanten Optimierungsprobleme zugeschnitten sind und diese effizient lösen. Industriepartner: Schaeffler Technologies GmbH & Co. KG |
| Prof. Günter Leugering, Dipl.-Technomath. Tobias Nuißl |
|
LeOpIn – Lebenszyklusoptimierung (2010-2013) Das Projekt LeOpIn (Lebenszyklusoptimierung für eine ressourcen- und energieeffiziente Infrastruktur) beschäftigt sich mit der Planung energieeffizienter Bürogebäude und Rohrleitungssysteme in Kraftwerken. |
|
Details LeOpIn setzt sich aus sechs Teilprojekten zusammen, von denen drei am Lehrstuhl für Angewandte Mathematik 2 angesiedelt sind. In der Planungsphase von größeren Bauprojekten werden üblicherweise nur Investitionskosten betrachtet. In der vorliegenden Machbarkeitsstudie hingegen wurde der gesamte Lebenszyklus von Gebäuden/Rohrleitungen in die optimale Planung mit einbezogen, um Aspekte wie akkumulierter CO2-Ausstoß und Nachhaltigkeit sehr viel stärker in die Entscheidungsfindung zu integrieren. Der Projektaufbau lässt sich am Fallbeispiel der Hochdruckrohrleitungen verdeutlichen: Nach einer physikalischen Feinmodellierung des Systems müssen die beschreibenden Modelle mit Hilfe modellreduktiver Verfahren für eine anschließende Optimierung aufbereitet werden. Bei der Feinmodellierung von Hochdruckrohrleitungen gilt es neben Erfassung von Statik und Dynamik von Stahlrohren auch das Langzeit-Materialverhalten zu beschreiben. Hierzu werden verschiedene Balkenmodelle, welche dünne eindimensionale Strukturen beschreiben, mit unterschiedlichen Materialmodellen, wie Thermoelastizität, Plastizität und Kriechschädigung, gekoppelt. Die entstehenden hochgradig nichtlinearen partiellen Differenzialgleichungen können mithilfe numerischer Verfahren am Computer gelöst werden.
Industriepartner: Bilfinger SE |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr. Michael Stingl (Erlangen), Dipl.-Technomath. Tobias Kufner (Erlangen), Dipl.-Technomath. Christoph Strohmeyer (Erlangen), Dipl.-Technomath. Maximilian Walther (Erlangen) |
|
Simulationsbasierte Optimierung In diesem Projekt werden allgemeine Optimierungsverfahren entwickelt, die einerseits theoretisch fundiert sind und andererseits vom Anwender ohne mathematisches Spezialwissen zur Optimierung von simulierten Prozesse angewendet werden können. |
|
Details Computersimulationen sind für viele Ingenieure, Entwickler, Forscher und Analysten in den letzten Jahren kaum noch wegzudenken. Ein Hauptgrund für die Simulation ist die Verbesserung der simulierten Prozesse. In diesem Projekt werden allgemeine Optimierungsverfahren entwickelt, die einerseits theoretisch fundiert sind und andererseits vom Anwender ohne mathematisches Spezialwissen zur Optimierung der simulierten Prozesse angewendet werden können. Das Hauptziel dieser Verfahren ist die Berechnung einer Lösung mit einer im Vergleich zu anderen Verfahren geringeren Anzahl an Simulationsläufen. Die bisher entwickelten Verfahren können auf – nichtlineare restringierte kontinuierliche Optimierungsprobleme und – nichtlineare kontinuierliche Gleichungs-/Ungleichungssysteme |
| Dr. Alexander Thekale (Erlangen), Dipl.Math. Markus Kaiser (Wuppertal), Prof. Dr. Kathrin Klamroth (Wuppertal), Philippe Toint (Namur,Belgien) |
|
Optimierung im Segelflug In diesem Projekt wurde für das Segelflug-Internetportal OnLineContest ein Algorithmus zur optimalen Auswahl von GPS Punkte entwickelt für die Berechnung der OLC-Classic Wertung. |
|
Details Segelflugzeuge sind heutzutage mit GPS-Geräten ausgestattet, die in Abständen von einigen Sekunden die Flugpositionen bestimmen. Somit sind Flugrouten durch in der Regel einige tausend Meßpunkte sehr genau bestimmt. Für Wertungsflüge in der OLC-Classic Wertung werden aus diesen Meßpunkten fünf bis sieben so ausgewählt, dass der gewichtete Streckenzug, der bei der Verbindung der ausgewählten Punkte entsteht, maximale Länge hat. In diesem Projekt wurde für das Segelflug-Internetportal OnLineContest ein Algorithmus zur optimalen Auswahl dieser Punkte entwickelt. Dabei wurde neben der garantierten Optimalität der Lösung eine Laufzeitverkürzung innerhalb der Optimierung von ca. 90% erzielt, was die Wartezeit der Segelflieger auf eine Bewertung ihres Fluges deutlich reduzierte. Dieser Algorithmus ist nun bei OnLineContest im Einsatz, weitere Wertungsformen werden zur Zeit optimiert. |
| Dr. Alexander Thekale (Erlangen), Prof. Dr. Kathrin Klamroth (Wuppertal), Martin Petz (OnLineContest) |
|
Optimierung der Zyklenanzahl im Full-Multigrid Algorithmus In diesem Projekt wurde ein spezieller Branch and Bound Algorithmus entwickelt, der die Anzahl der V-Zyklen im Full Multigrid Algorithmus optimiert |
|
Details Mehrgitterverfahren sind ein weit verbreitetes und effizientes Tool zur Lösung großer linearer Gleichungssysteme, die z.B. bei der Diskretisierung gewöhnlicher oder partieller Differentialgleichungen entstehen. In diesem Projekt wurde ein spezieller Branch and Bound Algorithmus entwickelt, der die Anzahl der V-Zykel im Full Multigrid Algorithmus optimiert, so dass signifikante Laufzeitverbesserungen erreicht wurde. |
| Dr. Alexander Thekale (Erlangen), Tobias Gradl (Erlangen), Prof. Dr. Kathrin Klamroth (Wuppertal), Prof. Dr. Ulrich Rüde (Erlangen) |





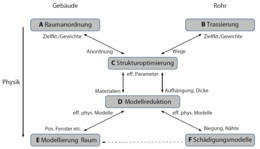
 tool geschaffen. Hierbei ist das Ziel, eine optimale Auswahl von Materialien und Komponenten hinsichtlich wirtschaftlicher und ökologischer Kriterien zu treffen. Im Anwendungsszenario Hochdruck-Rohrleitungen waren beispielsweise Stahlsorte und Durchmesser der Rohrelemente sowie Biegeradius und Winkel der Biegungen Gegenstand der Optimierung.
tool geschaffen. Hierbei ist das Ziel, eine optimale Auswahl von Materialien und Komponenten hinsichtlich wirtschaftlicher und ökologischer Kriterien zu treffen. Im Anwendungsszenario Hochdruck-Rohrleitungen waren beispielsweise Stahlsorte und Durchmesser der Rohrelemente sowie Biegeradius und Winkel der Biegungen Gegenstand der Optimierung. Das Beispiel der Bürogebäude lässt sich auf ähnliche Weise behandeln – mathematisch gesehen lassen sich beide physikalischen Systeme als Graphen darstellen. Dadurch besteht die Möglichkeit, die Methoden der Modellreduktion sowie die Optimierungsalgorithmen auch für die Planung und Optimierung von Gebäuden zu verwenden. Allein das zugrunde liegende physikalische Modell muss separat entwickelt werden.
Das Beispiel der Bürogebäude lässt sich auf ähnliche Weise behandeln – mathematisch gesehen lassen sich beide physikalischen Systeme als Graphen darstellen. Dadurch besteht die Möglichkeit, die Methoden der Modellreduktion sowie die Optimierungsalgorithmen auch für die Planung und Optimierung von Gebäuden zu verwenden. Allein das zugrunde liegende physikalische Modell muss separat entwickelt werden.