Projekte
Current projects
Interfaces, Complex Structures, and Singular Limits in Continuum MechanicsDFG Research Training Group GRK 2339/2Dates: 2022-2027 (second funding period), Mathematical models and methods are indispensable in natural and engineering sciences. The research training group „IntComSin“ combines the expertise at FAU Erlangen- Nürnberg and at University of Regensburg in (S)PDE-analysis, calculus of variations, homogenisation and Gamma-convergence, numerical analysis and scientific computing to set up a unique research and training center to investigate at the highest scientific level selected phenomena and processes, which are related to interfaces, multiple scales/fields, and dimension reduced models arising as singular limits. This way, the research training group responds to the still growing demand for refined mathematical models, their thorough analysis and efficient numerical implementation, their predictive power and potential of optimisation which arises in various fields of natural sciences, medicine, and engineering (biology, cardiology and oncology, materials sciences, manufacturing technology). Questions under consideration are currently of major interest both from a mathematical point of view and from an application perspective and are related to the guiding topics of the RTG: – INTERFACES which separate states of different properties in materials and occur, e.g., in multi-phase flow in fluid dynamics, in fluid-structure interactions in arterial blood flow, as free boundaries in tumour growth or in the macroscopic description of interacting species. – COMPLEX STRUCTURES in porous media, in elastic media with fine-scale structures, or in non-classical fluids, for which the presence of microstructures — like polymers — causes non-standard flow behaviour. – SINGULAR LIMITS related to small length scales in models of continuum mechanics (e.g. elastic plates or rods or thin liquid films) which give rise to dimension reduced models of lower computational complexity. For further information, see https://intcomsin.de |
Completed projects
Interfaces, Complex Structures, and Singular Limits in Continuum MechanicsDFG Research Training Group GRK 2339Dates: 2018-2022 (first funding period), The DFG Research Training Group IntComSin is a joint |
Free boundary propagation and noise: analysis and numerics of stochastic degenerate parabolic equationsDFG Research Grant
The porous-medium equation and the thin-film equation are prominent examples of nonnegativity preserving degenerate parabolic equations which give rise to free boundary problems with the free boundary at time t > 0 defined as the boundary of the solution’s support at that time. |
Diffusive interface models for transport processes at fluidic interfaces (Part 2)DFG Priority Programme SPP 1056 „Transport processes at fluidic interfaces“ |
||||
|
Fronts and Interfaces in Science and Technology (FIRST) / Marie Curie Initial Training Networks |
||||||
|
Diffusive interface models for transport processes at fluidic interfaces (Part 1)DFG Priority Programme SPP 1056 „Transport processes at fluid interfaces“ |
||||
Topological transitions like droplet coalescence or droplet break-up are fundamental features of two-phase flows. In recent years, diffuse interface models turned out to be a promising approach to describe such phenomena. Species transport across fluidic interfaces and the effects exerted by soluble and insoluble surfactants are additional issues of still increasing technological importance.
|
Mathematical Analysis of Models Describing the Evolution of Liquid Patterns on Material Interfaces (Part 2 and Part 3)DFG Priority Programme SPP 1052 „Benetzung und Strukturbildung an Grenzflächen““ |
||||
|
DAAD project „Mathematical Analysis and Numerical Simulation of Dynamic Electrowetting“ („projektbezogener Personenaustausch Spanien“) |
||||||
Electric fields may influence the wetting behaviour of charged droplets. This effect may be used to manipulate droplet motion and to enforce droplet coalescence or break-up. It is summarized under the notion of electrowetting. First studied in the late 19th century by Lippmann and others, very recently this effect gained the interest of physicists and engineers on account of a variety of applications in micro-fluidics („lab-on-a-chip“). However, mathematical modeling of this effect is still in its childhood — the dependency of contact angles on the applied voltage is modeled by the so called Lippmann formula which may hold true at most in a small voltage regime. In this project, new thermodynamically consistent models shall be derived to describe the evolution of droplet, voltage and thereby to shed light on the mechanisms underlying electrowetting. Existence of solutions shall be proven and efficient numerical schemes shall be developed as well. Poster>>
|
Complex rheologiesProject in SFB 611 „Singular phenomena and scaling in mathematical models“, University of Bonn (together with Christiane Helzel and Felix Otto) |
||
In this project, models for complex flow phenomena are investigated, for instance pattern formation in sheared suspensions, moving contact lines or Rayleigh-Bénard convection. By means of rigorous analysis and numerical simulations, properties of the models will be predicted. The aforementioned specific models may be used to develop new methods for PDE in general.
|
Scaling laws and their cross-overs: global analysis of rheological processesProject in SFB 611 „Singular phenomena and scaling in mathematical models“, University of Bonn (together with Felix Otto) |
||
The goal of this project is to investigate scaling laws in rheological processes. More precisely, analytical tools to rigorously infer such scaling laws shall be developed. A common feature of the friction dominated processes to be investigated is their gradient flow structure. This structure translates the physical free energy and the underlying dissipation mechanism into the mathematical terms of functional and metric tensor, respectively. The idea is to use global PDE methods, rather than local methods, like matched asymptotic expansions, to analyze the scaling laws. Phenomena to be studied include spreading of viscous films, case-II diffusion of solvents in polymeric solids, and the demixing of polymer solutions and sponge-like pattern formation.
|
DFG project „Mathematical Analysis of Models Describing the Evolution of Liquid Patterns on Material Interfaces „)Project in SFB 611 DFG Priority Programme SPP 1052 „Benetzung und Strukturbildung an Grenzflächen“ |
||||
|

 doctorate program of FAU and University of Regensburg in Applied Mathematics. The research focuses on many aspects of advanced mathematical modeling, analysis and numerics with the perspective to understand complex phenomena observed in fluid mechanics, material engineering, biological systems and other applied sciences. Typically interfaces, multiple scales/fields and small parameters (singular limits) are the core features of the problems to be studied. The doctoral program offers a structured course program in partial differential equations, calculus of variations, numerical analysis, scientific computing, mathematical modeling and professional skills. The topics explored in the doctoral projects address:
doctorate program of FAU and University of Regensburg in Applied Mathematics. The research focuses on many aspects of advanced mathematical modeling, analysis and numerics with the perspective to understand complex phenomena observed in fluid mechanics, material engineering, biological systems and other applied sciences. Typically interfaces, multiple scales/fields and small parameters (singular limits) are the core features of the problems to be studied. The doctoral program offers a structured course program in partial differential equations, calculus of variations, numerical analysis, scientific computing, mathematical modeling and professional skills. The topics explored in the doctoral projects address: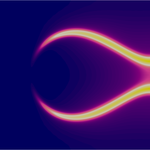 In recent years, diffuse interface models turned out to be a promising approach to describe fundamental features of two-phase flow like droplet break-up or coalescence. In the second funding period, novel thermodynamical consistent phase-field models for species transport in two-phase flow shall be derived with an emphasis on soluble surfactants. Additional phenomena — ranging from microscale effects like molecule orientation over thermal effects to electrostatic interactions — shall be included as well. On this basis, new sharp-interface models shall be derived by formal asymptotic analysis.
In recent years, diffuse interface models turned out to be a promising approach to describe fundamental features of two-phase flow like droplet break-up or coalescence. In the second funding period, novel thermodynamical consistent phase-field models for species transport in two-phase flow shall be derived with an emphasis on soluble surfactants. Additional phenomena — ranging from microscale effects like molecule orientation over thermal effects to electrostatic interactions — shall be included as well. On this basis, new sharp-interface models shall be derived by formal asymptotic analysis.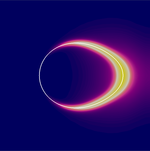 For selected diffuse-interface models, existence of solutions and stability of fluidic interfaces will be investigated by rigorous mathematical analysis. Stable numerical schemes shall be formulated and implemented in two and three space dimensions. By numerical simulations, partially guided by the „Leitmassnahme“ Taylor-flow, the models shall be validated and further improved. By numerical analysis, convergence shall be established for the prototypical problem of species transport in two-phase flow with general mass densities.
For selected diffuse-interface models, existence of solutions and stability of fluidic interfaces will be investigated by rigorous mathematical analysis. Stable numerical schemes shall be formulated and implemented in two and three space dimensions. By numerical simulations, partially guided by the „Leitmassnahme“ Taylor-flow, the models shall be validated and further improved. By numerical analysis, convergence shall be established for the prototypical problem of species transport in two-phase flow with general mass densities. With this network, the universities of Bath, Eindhoven, Erlangen, Haifa (Technion), Madrid (Complutense), Paris (Orsay), Rome (La Sapienza), Zürich and the industrial partners EGIS and SIEMENS AG foster a joint training platform for PhD-students working on analysis and control of interfacial phenomena. Applications range from image processing over reaction-diffusion systems to complex multi-phase flow.
With this network, the universities of Bath, Eindhoven, Erlangen, Haifa (Technion), Madrid (Complutense), Paris (Orsay), Rome (La Sapienza), Zürich and the industrial partners EGIS and SIEMENS AG foster a joint training platform for PhD-students working on analysis and control of interfacial phenomena. Applications range from image processing over reaction-diffusion systems to complex multi-phase flow.



 The goal of the project is to analyse, to evaluate, and to improve mathematical models for the dewetting of thin liquid films on homogeneous surfaces and the formation of fluid structures on inhomogeneous substrates. During the second period of the Schwerpunktprogramm, investigations on evaporation and condensation processes will be included. The proposed project consists of three main parts which can be summarized as follows:Modelling: Based on lubrication approximation, evolution equations for the height of condensing fluids on inhomogeneous surfaces shall be derived.Analysis: Methods from the calculus of variations and the theory of partial differential equations shall be used to obtain results on existence and qualitative behaviour of solutions to the corresponding evolution equations for film height h and pressure p. Besides their obvious importance for a better understanding of the asymptotic behaviour of solutions, these theoretical results are also the key ingredient to formulate fast and reliable algorithms for numerical sumulations.Numerical simulations: During the last two years, G. Grün and M. Rumpf succeded in developing and analysing a finite-element/finite-volume scheme which drastically reduces the computation time for the simulation of spreading phenomena. Based on this scheme, a general finite-element solver shall be designed to enable numerical simulations of all the phenomena mentioned above. The evaluation will be performed by comparison with experimental data; it strongly depends on an intense cooperation with experimentalists inside the Schwerpunktprogramm.
The goal of the project is to analyse, to evaluate, and to improve mathematical models for the dewetting of thin liquid films on homogeneous surfaces and the formation of fluid structures on inhomogeneous substrates. During the second period of the Schwerpunktprogramm, investigations on evaporation and condensation processes will be included. The proposed project consists of three main parts which can be summarized as follows:Modelling: Based on lubrication approximation, evolution equations for the height of condensing fluids on inhomogeneous surfaces shall be derived.Analysis: Methods from the calculus of variations and the theory of partial differential equations shall be used to obtain results on existence and qualitative behaviour of solutions to the corresponding evolution equations for film height h and pressure p. Besides their obvious importance for a better understanding of the asymptotic behaviour of solutions, these theoretical results are also the key ingredient to formulate fast and reliable algorithms for numerical sumulations.Numerical simulations: During the last two years, G. Grün and M. Rumpf succeded in developing and analysing a finite-element/finite-volume scheme which drastically reduces the computation time for the simulation of spreading phenomena. Based on this scheme, a general finite-element solver shall be designed to enable numerical simulations of all the phenomena mentioned above. The evaluation will be performed by comparison with experimental data; it strongly depends on an intense cooperation with experimentalists inside the Schwerpunktprogramm.  This project is concerned with the analytical description of the qualitative and asymptotic behaviour of solutions to certain higher order parabolic differential equations arising in modelling phenomena of wetting and film rupture. It is planned to develop efficient numerical tools — in particular algorithms based on Finite-Volume-Methods — to enable computer simulations of film rupture in space dimension N = 3.
This project is concerned with the analytical description of the qualitative and asymptotic behaviour of solutions to certain higher order parabolic differential equations arising in modelling phenomena of wetting and film rupture. It is planned to develop efficient numerical tools — in particular algorithms based on Finite-Volume-Methods — to enable computer simulations of film rupture in space dimension N = 3. — Part 2: Derivation and analysis of evolution equations to model the formation of liquid structures on inhomogeneous ma- terial interfaces.
— Part 2: Derivation and analysis of evolution equations to model the formation of liquid structures on inhomogeneous ma- terial interfaces.