Stochastic modelling of porous media
Stochastic modeling of transport processes in porous media |
||
The hydraulic conductivity in highly heterogeneous porous such as natural groundwater systems can be efficiently parameterized, mainly in large scale problems, merely as a space random function. Consequently, the modelled concentration transported in groundwater is random and stochastic predictive tools are required. The aim of our group is to develop robust numerical algorithms to solve evolution equations for the probability density function (PDF) of the random concentration field. This involves the formulation of the PDF equation for specific transport problems, solving large ensembles of transport problems which will be used for parameter calibrations and as reference stochastic solutions, and, finally, solving the PDF equation. The latter uses consistency constraints which render the PDF equation equivalent to a Fokker-Planck equation and to its Itô process representation. The systems of the resulting Itô equations is solved by tracking computational particles in physical and concentration spaces with a global random walk algorithm (GRW), stable, free of numerical diffusion, and insensitive to the increase of the number of particles. |
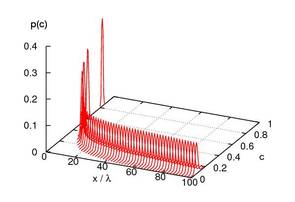
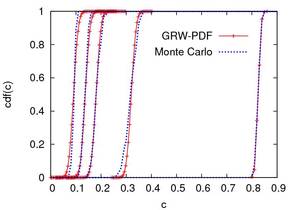
Probability density functions (up) and corresponding cumulative distribution functions (down) of the concentration of a passive scalar transported along the mean flow trajectory in a saturated aquifer with hydraulic conductivity modelled as a space random function.