Seminar Zopfgruppen und Knotentheorie
Seminar Niedrigdimensionale Topologie: Zopfgruppen und Knotentheorie
Wintersemester 2021/22
- Univis: Als Bachelorseminar Topologie und als Seminar zum Querschnittsmodul Topologie.
⚠ Der wöchentliche Termin ist noch nicht definitiv fixiert. - StudOn-Link mit Liste der noch verfügbaren Vortragsthemen (unter „Info“)
Dieses Seminar befasst sich mit zwei miteinander verwandten Themen der niedrigdimensionalen Topologie: Zöpfen und Knoten/ Verschlingungen. Diese erscheinen zunächst als geometrische Gebilde, wie sie in diesem Bild links (Zöpfe) bzw. rechts (Verschlingung = Knoten mit mehreren Komponenten) dargestellt sind:
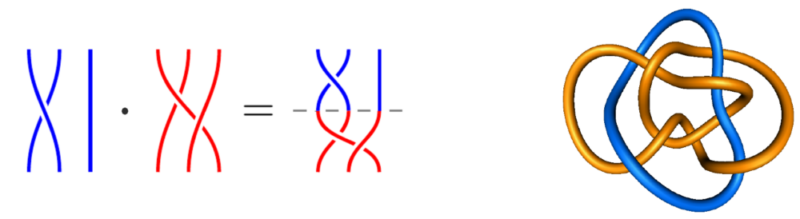
Man stellt sich hier die Stränge/Fäden als beliebig elastisch vor und unterscheidet nicht zwischen Objekten, die durch stetige Deformationen auseinander hervorgehen, so dass jede Grafik ein zugrundeliegendes topologisches Objekt darstellt. Eine zentrale Frage ist, eine mathematische Beschreibung von Eigenschaften dieser Objekte zu finden, die ebenfalls unter stetigen Deformationen invariant sind, also Eigenschaften der zugrundeliegenden topologischen Zöpfe/Knoten reflektieren.
Im Laufe der Vorträge werden Sie viele Aspekte von topologischen Zöpfen und Knoten kennenlernen, die mit diversen anderen Themen in Zusammenhang stehen. Zöpfe bilden eine Gruppe (siehe Bild oben links für die Idee der Komposition in dieser Gruppe), die sogenannte Zopfgruppe, so dass hier ein Bezug zur Gruppentheorie entsteht. Das Studium der Struktur der Zopfgruppen und ihrer Darstellungen hat Verbindungen zur Algebra und Darstellungstheorie, und die Charakterisierung von Zopfgruppen als Fundamentalgruppen bezieht sich direkt auf die Topologie-Vorlesung. Bei der Diskussion von Knoteninvarianten werden wir aber auch auf kombinatorische Aspekte und Anknüpfungspunkte mit Operatoralgebren stoßen (in diesem Zusammenhang wurde das berühmte Jones-Polynom ursprünglich entdeckt).
Anwendungen gibt es unter anderem in der Kryptographie, Biologie (DNA), und der Quantenphysik. Der Fokus des Seminars wird aber auf der Seite der reinen Mathematik liegen.
- Seminarankündigung mit Liste der Themen und Literatur.
- Untechnischer Artikel (Oberwolfach Snapshot) als Einführung.
- Einige Themen bieten die Möglichkeit, eine Bachelorarbeit anzugliedern, insbesondere Vortrag 12 (Die Temperley-Lieb Algebra), 13 (Die Temperley-Lieb Algebra und das Jones-Polynom), und 14 (Erweiterte Yang-Baxter Operatoren und Knoteninvarianten)
